从苯分子到碳纳米结构：成键熵模型的直观理解

要理解碳纳米结构中的原子间相互作用，我们不妨从最简单的苯分子谈起。

1. 从苯分子的共振说起

苯分子中存在两种交替的单、双键排布形式，即著名的 Kekulé 结构。
这两种形式彼此等价，拥有三重对称性，但它们却违背了实验事实：在实际苯分子中，所有 C–C 键的长度和强度是相同的。

如何解决这个矛盾？
答案是：共振。
苯的真实基态并不是某一个固定的 Kekulé 结构，而是两种结构的等权叠加。
这种叠加带来了额外的“共振能量”，使体系更稳定。
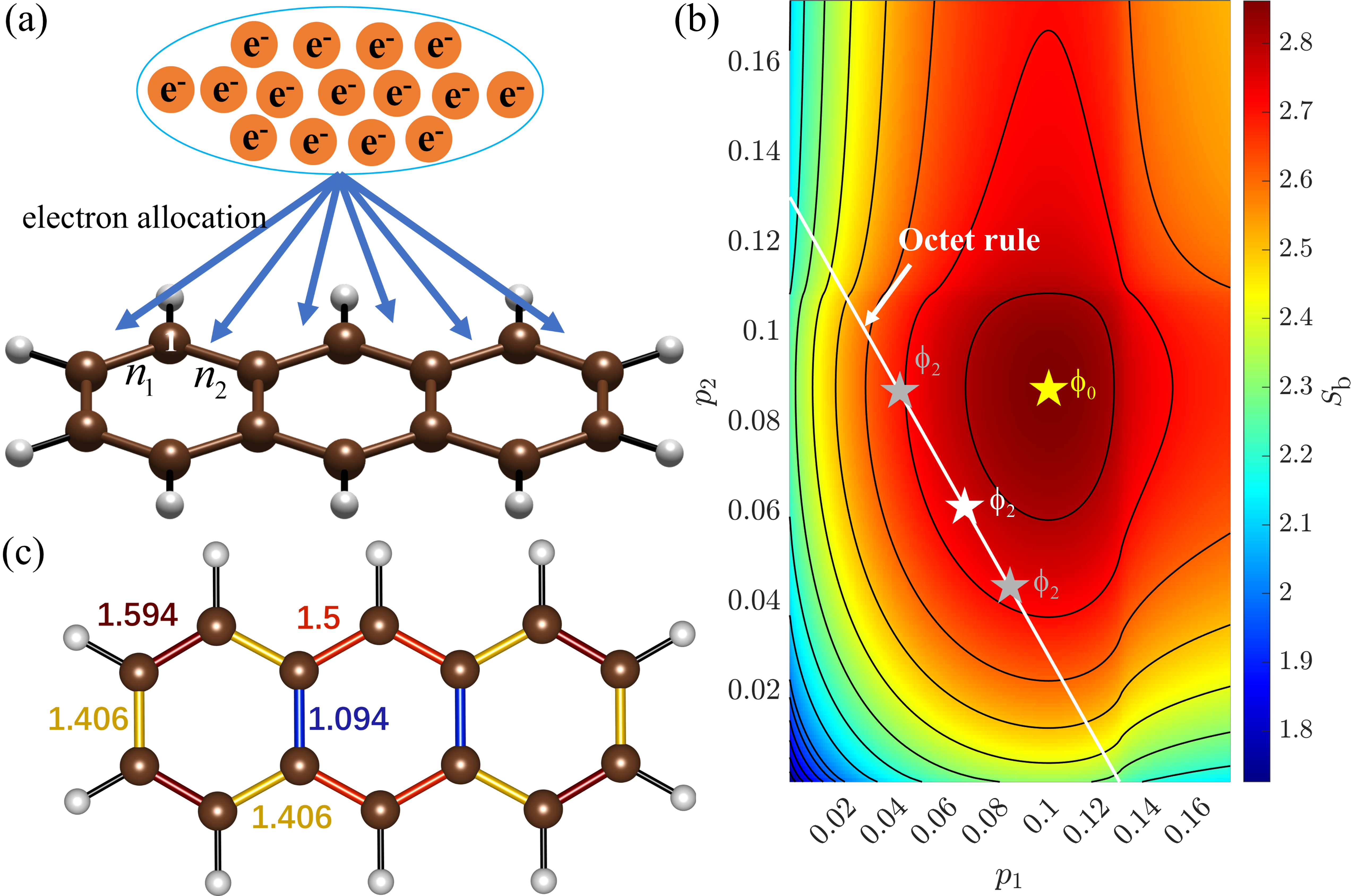
在这种状态下，每个 C–C 键的成键序数（ON）都等于 1.5，完美符合从量子化学计算（如 DFT）得到的电荷密度分布。

换句话说，苯的最优态就是两种 Kekulé 结构的叠加，权重相同（即 1/√2）。

2. 推广到更大分子

如果我们把视野扩展到更大的分子，例如 蒽（anthracene），情况就复杂了。
蒽拥有四种 Kekulé 结构。
量子化学计算表明：蒽分子边缘的 C–C 键比内部的 C–C 键更强。
然而，要准确计算出这些键的成键序数（ONs）却非常困难，通常只能依赖昂贵的第一性原理计算（DFT 等）。

3. 成键熵模型（Bonding Entropy Model, BEM）

为了解决这个问题，研究者提出了 成键熵模型。
核心思想非常优雅：

• 在满足八隅体规则的前提下，一个碳纳米结构可能对应若干种退化的 Kekulé 结构。
• 假设电子可以在所有可能的化学键之间自由离域，那么每条键上的电子数 \(n_i\) 就是可变的。
• 整个体系的电子总数 \(N_\text{total}\) 需要分配到所有键上。

在这种框架下，体系自然会趋向于最均匀的电子分布，因为这对应着最大化的 Shannon 熵：

也就是说，系统会通过熵的最大化来增强电子离域、获得额外的稳定性。
最终，最优的电子分布就是使成键熵达到最大值的那一种。

4. 为什么重要？

• 这个模型把复杂的量子问题转化为一个直观的统计物理图像：
  电子倾向于“平均分布”，从而让体系更稳定。
• 它能够用非常简单的方式解释为什么不同的碳纳米结构会表现出不同的键强分布和磁性。
• 相比传统依赖大规模量子计算的方法，成键熵模型更轻量化、解释力更强，也为未来预测碳基新材料提供了有趣的工具。

✨ 从苯的共振，到蒽的多重 Kekulé 结构，再到复杂的碳纳米片，成键熵模型给我们提供了一种新的视角：
熵并不仅仅是热力学量，它还是理解分子稳定性的关键钥匙。

成键熵模型（BEM）：揭示石墨烯纳米片的磁性之谜

石墨烯一直以来是凝聚态物理和材料科学中的明星材料。
在纳米尺度下，石墨烯片段（Graphene Nanoflakes, GNFs）会因为 量子限域效应、边缘效应和拓扑挫折 而展现出丰富的磁性现象。

这篇研究工作提出了一个新的理论框架——成键熵模型（Bonding Entropy Model, BEM），用来统一解释不同类型石墨烯纳米片的磁性来源。

研究背景

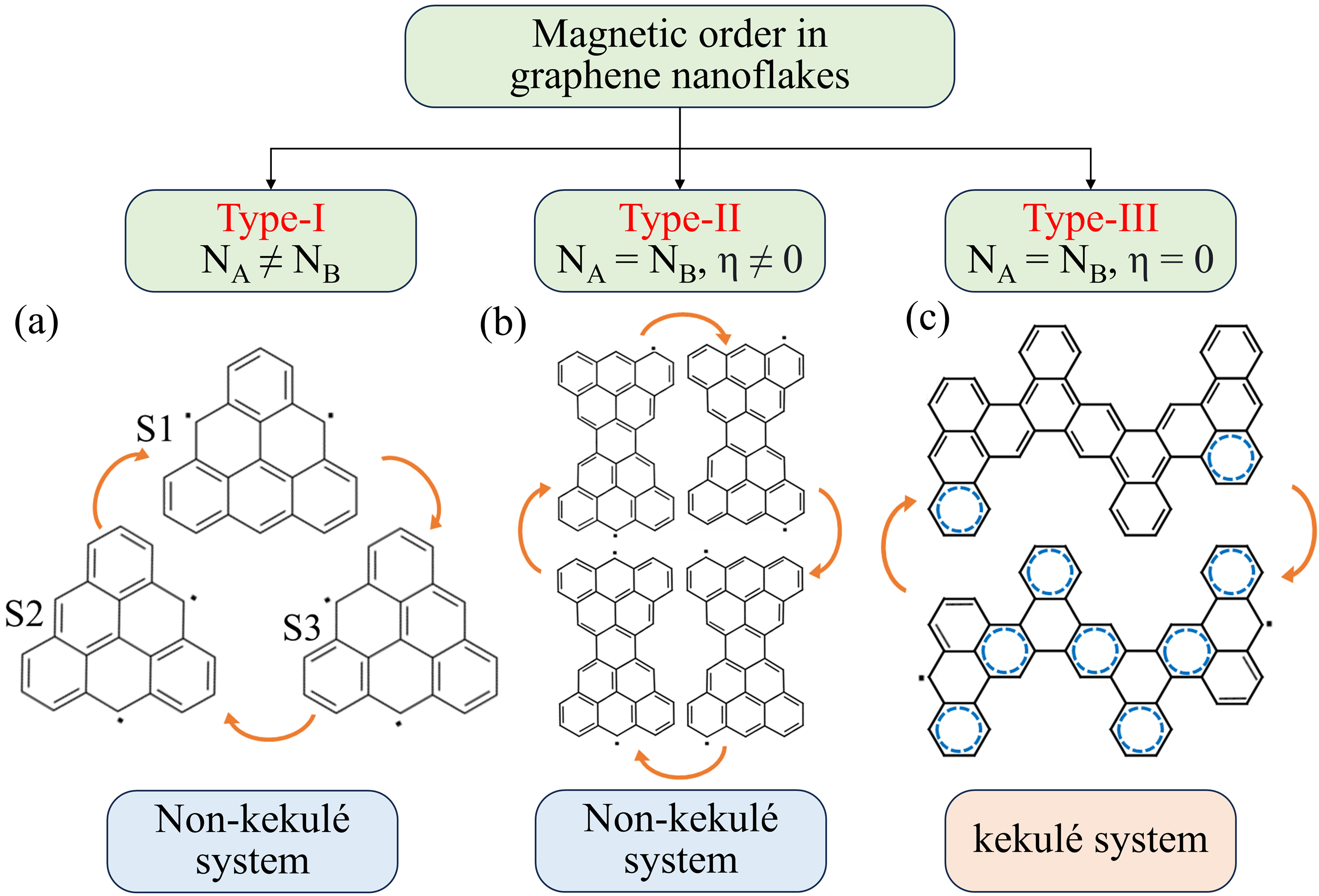
• 非-Kekulé 结构 的磁性主要来源于亚晶格不平衡导致的未成对电子。
• Kekulé 型结构 的磁性则可能来自于芳香性稳定与电子成对化之间的竞争。

然而，传统理论模型在同时解释这两类结构的电子分布、磁矩分布以及稳定性时，往往存在局限。

研究方法：成键熵模型（BEM）

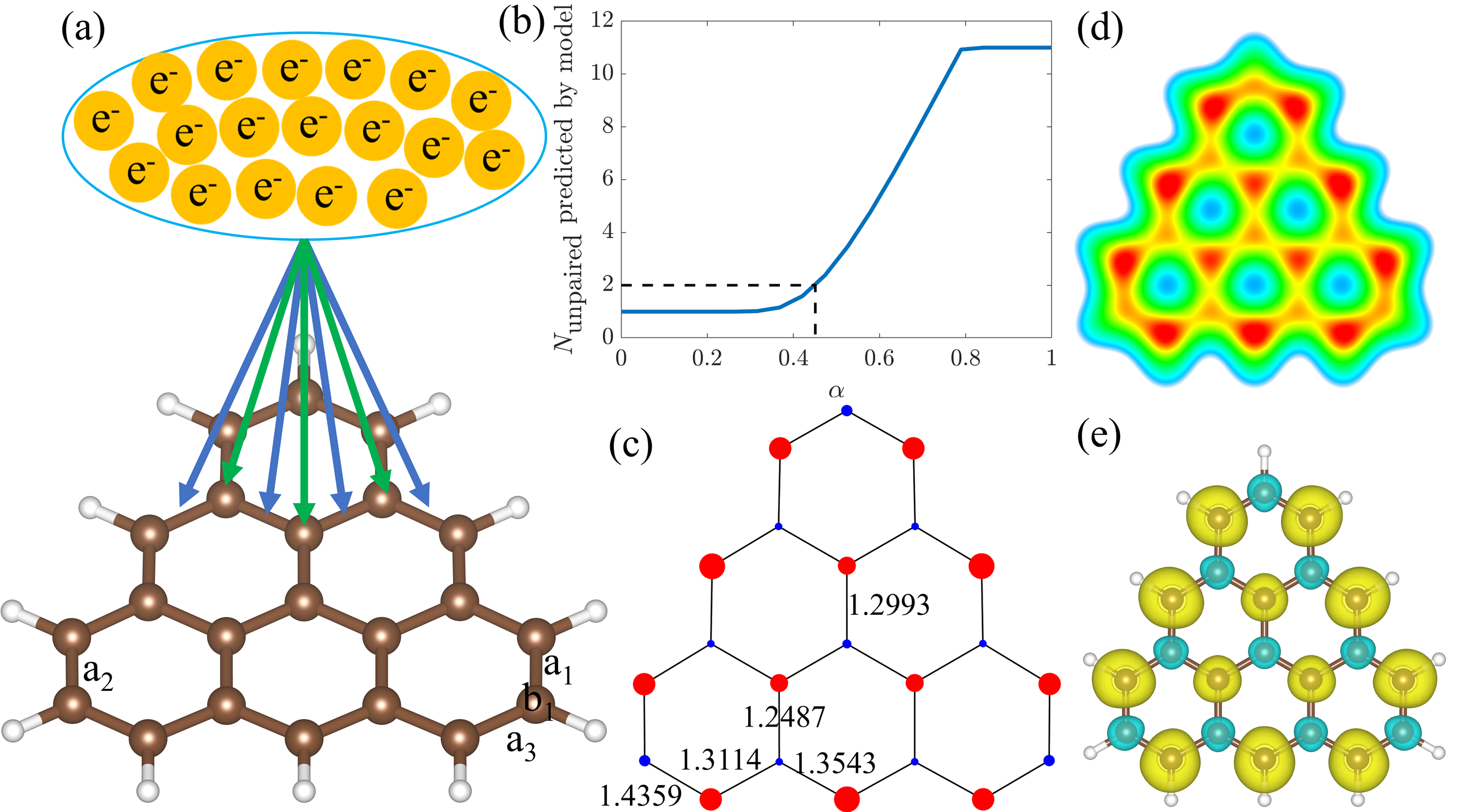
BEM 的核心思想是：
在价电子数的约束下，体系会趋向于最大化成键熵，从而获得最稳定的电子分布。

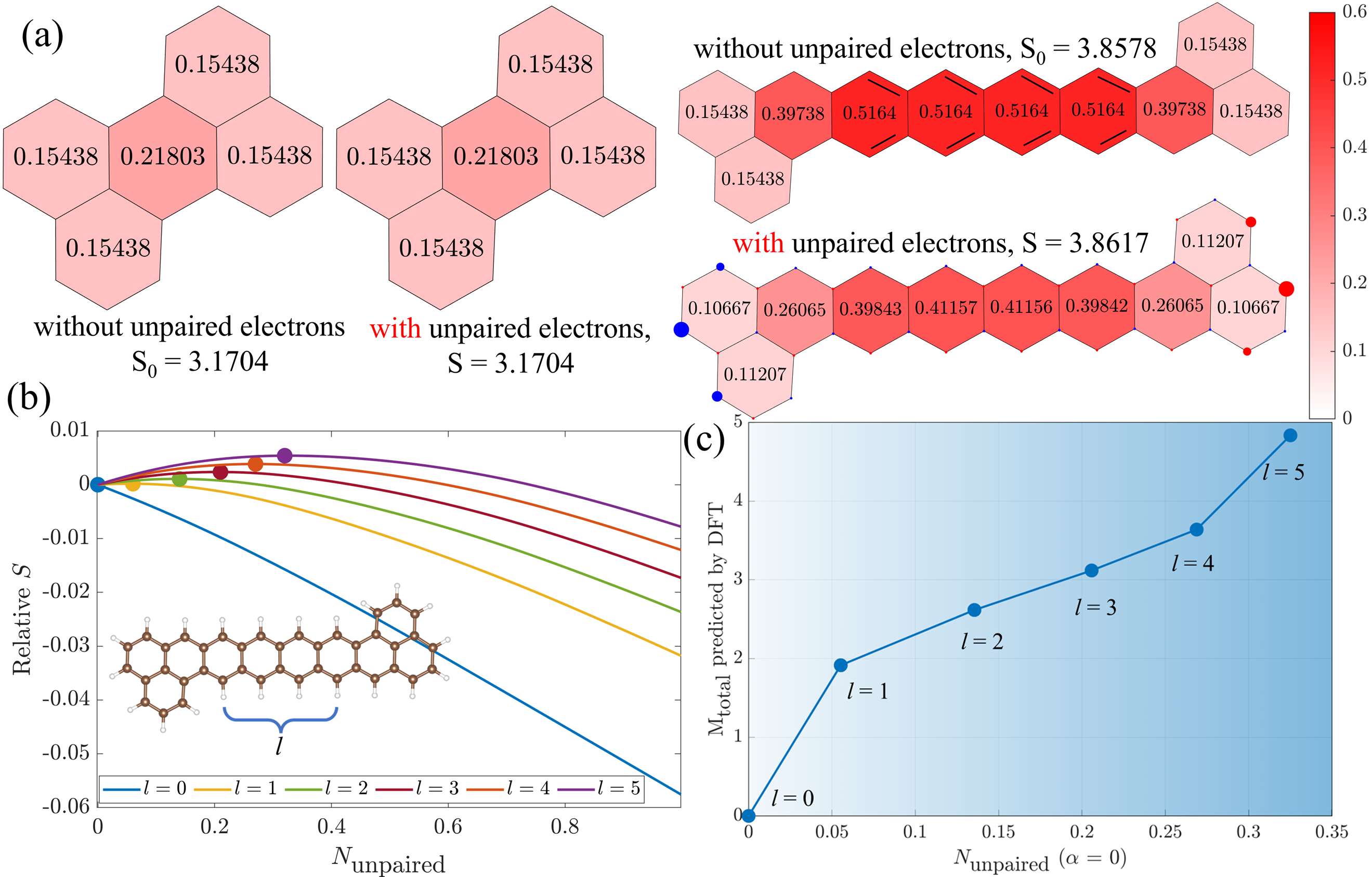
• 通过最大化成键熵，可以预测 C–C 键的占据数 与 局域磁矩分布。
• 在模型中，电子分配到化学键与未成对电子之间有一个权重系数 α，其数值由体系的未成对电子数唯一决定。
• 这个方法不依赖额外的拟合参数，既适用于 非-Kekulé 系统，也适用于 Kekulé 系统。

主要结果

1. 模型准确性

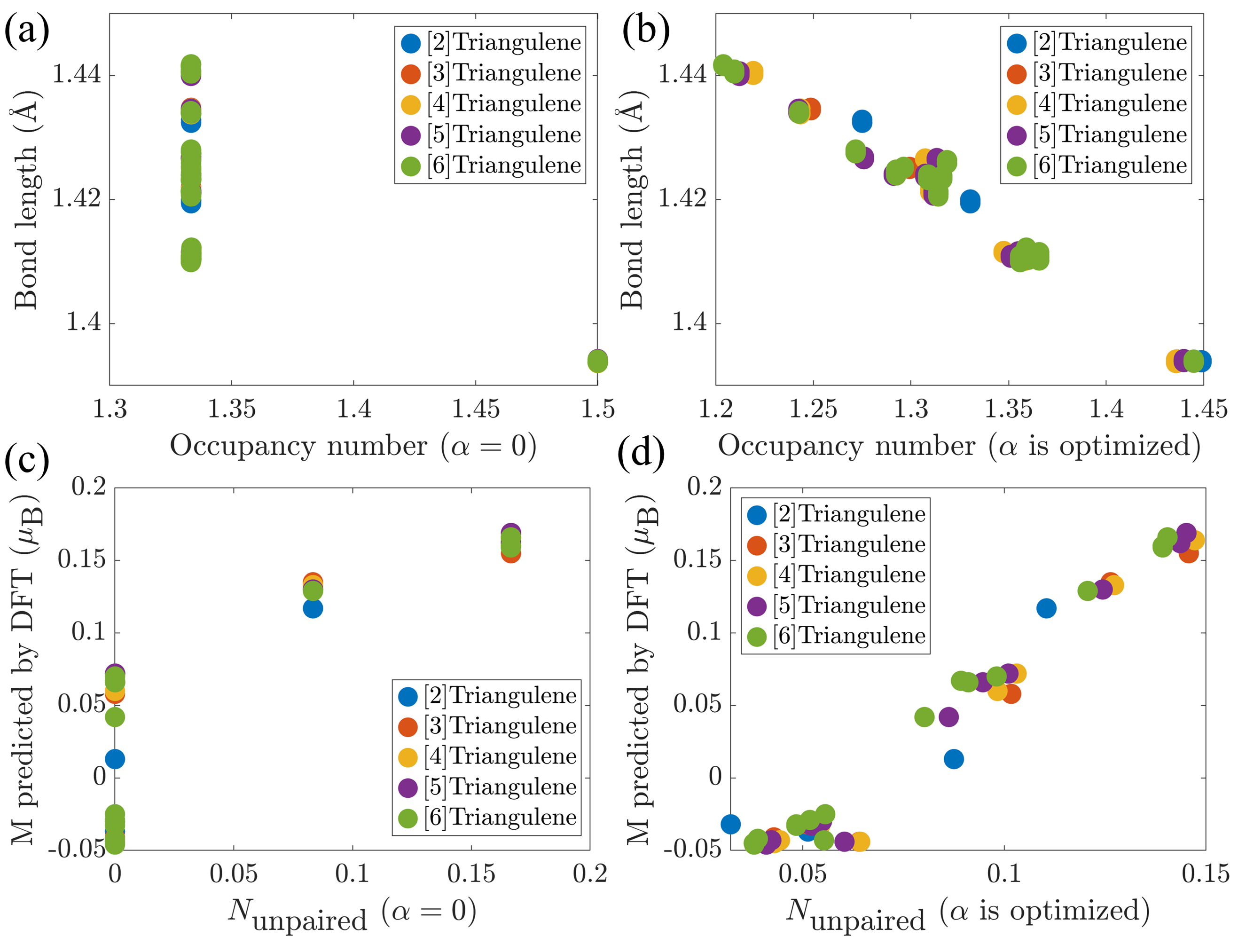
• 对典型分子（如 [3]triangulene、Clar’s goblet 以及 Kekulé 自由基），BEM 预测的电子密度分布、未成对电子数和局域磁矩与 DFT 结果高度一致。
• 模型揭示：占据数与 C–C 键长呈线性关系，体系总能量与成键熵也高度相关。
  

2. 分类与物理机制

• 非-Kekulé 系统（类型 I 和 II）：磁性源自亚晶格不平衡或拓扑挫折。
• Kekulé 系统（类型 III）：当未成对电子带来的熵增和芳香性增益超过成对化倾向时，磁性得以出现。
• 当 α = 0 时，成键熵的行为可用来判断体系是否倾向于磁性。

3. 结构稳定性预测

• 成键熵越大 → 电子分布越均匀 → 芳香性越强 → 结构越稳定。
• BEM 能有效识别由于氢原子位阻或磁矩排布导致的不稳定构型。

4. Kekulé 系统的磁性转变

• 对某些 Kekulé 分子，若开放壳层（存在未成对电子），会提高成键熵并增强芳香性，从而获得更稳定的结构。
• 模型预测的未成对电子数与 DFT 计算得到的总磁矩呈现线性关系。
  

结论与意义

• BEM 提供了一个统一、直观且高效的统计框架，能够定量描述不同类型石墨烯纳米片的电子分布与磁性。
• 成键熵不仅揭示了磁性机制，还可作为设计可调磁性的碳基材料的一般原则。
• 这为 自旋电子学材料 的发现和设计提供了新的思路与方法。

✨ 总结来说，BEM 用“熵”的视角，搭起了一座连接量子化学与材料磁性的桥梁。
未来，基于成键熵的思路或许能帮助我们发现更多具有可控磁性的低维碳基材料。

参考文献

[1] Chang-Chun He, Shao-Gang Xu, Jiarui Zeng, Weijie Huang, Yao Yao, Yu-Jun Zhao, Hu Xu, and Xiao-Bao Yang. J. Chem. Phys. 162, 154104 (2025).
[2] Chang-Chun He, Shao-Gang Xu, Yu-Jun Zhao, Hu Xu, and Xiao-Bao Yang. Phys. Rev. B 111, 085408 (2025).
[3] Hai-Wei Luo, Chang-Chun He, Yu-Jun Zhao, Xiao-Bao Yang†. J. Chem. Phys. 163, 074701 (2025).